Pubblicato il 23 novembre 2018
ANATOCISMO NEI PIANI DI AMMORTAMENTO ALLA FRANCESE: LA GIURISPRUDENZA INIZIA A RICONOSCERE LA MATEMATICA
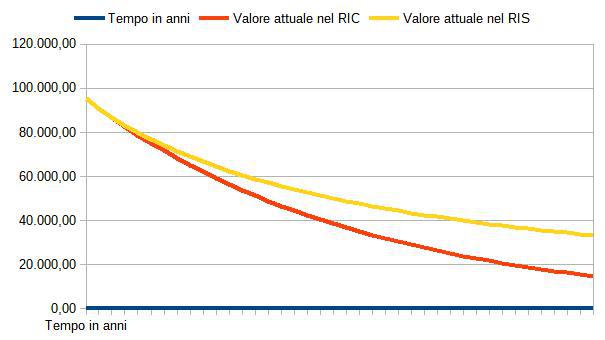
Breve analisi della sentenza n. 1558/2018 del 13 febbraio 2018 del Tribunale di Napoli. (Est. Alinante)
La questione relativa alla presenza di anatocismo nei comuni piani di ammortamento “a rata costante” o “alla francese”, dopo essere stata per lungo tempo liquidata come questione prima di fondamento comincia ad essere trattata finalmente secondo il suo giuto peso. Ad oggi infatti, la Giurisprudenza chiamata a pronunciarsi nel merito della questione, ha in larga parte negato la presenza di anatocismo nel piano di ammortamento alla francese.
Ultimamente tuttavia pare che questo orientamento, finora scalfito solo da alcune sentenze rimaste isolate, di cui la prima quella del Tribunale di Bari (sez. staccata di Rutigliano, 29 ottobre 2009, Giudice Mastronardi), stia cambiando.
Complici infatti delle consulenze tecniche ben fatte e argomentate, i Giudici di ben due Tribunali hanno riconosciuto la presenza di anatocismo nel piano di ammortamento alla francese: una è del 10 maggio 2018 (Tribunale di Lucca sent. n. 763/2018 del 10 maggio, 2018. Est. Mancini) e l’altra di qualche mese prima, del Tribunale di Napoli (sent. n. 1558/2018 del 13 febbraio 2018, Est. Alinante).
Quest’ultima, merita una attenta analisi, sia per l’importanza del Foro giudicante, sia per lo spessore delle argomentazioni tecniche a supporto delle motivazioni della sentenza, che brevemente si riportano:
“[…]Il CTU ha poi mostrato nella sua relazione che, nel piano di ammortamento del mutuo per cui è causa, ad ogni scadenza, gli interessi maturati vengono di fatto dapprima addebitati al capitale e poi pagati nella quota contenuta nella rata. In tal modo, quindi, come evidenziato nella tabella, gli stessi interessi continuano a partecipare al computo degli interessi proprio perché sono stati capitalizzati.
Tale dimostrazione è analitica ed accompagnata da specifiche tabelle che sviluppano quantitativamente la tesi del CTU, alla quale il CT di parte della Banca non ha saputo contrapporre argomentazioni altrettanto analitiche, non avendo nemmeno preso in considerazione i calcoli del CT[…]”.
Fermo restando quindi come sia pacifico che l’anatocismo, ovvero la capitalizzazone periodica (anche con cadenza annuale) degli interessi sui rapporti di finanziamento diversi dal conto corrente sia vietato dall’ordinamento, per capire le motivazioni (e la portata) della sentenza in commento, bisogna indagare sulla struttura matematica di un piano di ammortamento alla francese (redatto in regime di interessi composto ndr) e verificare se è vero che vi è capitalizzazione degli interessi.
BREVE ANALISI TECNICA DELL’AMMORTAMENTO ALLA FRANCESE (redatto in regime di interessi composti)
In matematica, si definisce mutuo una operazione finanziaria conforme allo schema seguente:
All’epoca iniziale t=0 un soggetto (mutuante o creditore) cede ad un secondo soggetto (mutuatario o debitore) un importo S (importo del mutuo o prestito), che viene frazionato negli importi non negativi (quote capitale), che vengono corrisposti alle scadenze
in maniera tale che si verifichi la (condizione di chiusura semplice):
(formula 1.0)
Sulla somma ottenuta in prestito il mutuatario deve corrispondere degli interessi, maturati per ogni scadenza sul debito residuo ad un determinato d’interesse i. Se si utilizza il regime composto, l’importo della rata (costante) risulta determinato secondo la formula seguente (per approfondimenti si rimanda alla bibliografia):
![]()
(formula 1.1)
Ciò comporta che, ad ogni scadenza di rata, il cui numero generico indicheremo con k, (k è l’indice di rata generico e varia da 1 ad n dove n è il numero dell’ultima rata prevista dal piano di ammortamento), il mutuatario debba adempiere due distinte ma correlate obbligazioni, versando al mutuante:
-
-
la k-esima quota di capitale, che indicheremo con Ck
-
la k-esima quota interessi, Ik, che riguarda gli interessi maturati sul debito residuo al tasso d’interesse i in vigore tra le due epoche successive
e
-
Sicché risulta che ciascuna rata è composta da una quota capitale ed una quota interessi, in maniera tale che risulti sempre verificata la seguente equazione:
(formula 1.2)
BREVE VERIFICA MATEMATICA DELL’ANATOCISMO
Con il pagamento di ogni rata di importo Rk, da corrispondere a ciascuna scadenza, al debitore viene quindi chiesto il rimborso del capitale e, contestualmente, anche degli interessi maturati sul debito residuo risultante dopo il pagamento della rata immediatamente precedente.
Se S è il capitale mutuato, ed n il numero delle rate, il debito residuo, che indicheremo genericamente con Dk all’epoca iniziale sarà pari ad S, mentre immediatamente dopo il pagamento della prima rata risulterà essere pari a
Sicché, per ciascuna scadenza k-esima risulterà:
(formula 1.3)
La formula 1.3 dice che “dopo il pagamento della rata Rk scadente all’epoca tk, il debito residuo risultante sarà pari alla differenza tra il capitale inizialmente mutuato (o prestato), indicato con S e la somma di tutte le quote capitali, da quella pagata con la Rata 1 a quella pagata con la Rata k-esima“.
Dalla 1.3, eliminando la sommatoria, risulta facile determinare il Debito residuo ad ogni scadenza, dopo cioè il pagamento della rata k-esima come risultante dall’equazione:
(formula 1.4)
IL CALCOLO DELLA QUOTA INTERESSI
Nell’ammortamento francese (in regime di interessi composto), ciascuna quota intessi, (cfr. la 1.2) risulta determinata attraverso la seguente relazione matematica:
(formula 1.5)
dove: ik è il tasso d’interesse periodale in vigore tra le due scadenze consecutive.
Ora: dalla 1.2 è possibile, mediante un semplice passaggio algebrico, determinare l’importo di ciascuna quota capitale da pagare ad ogni rata k-esima come risultato della seguente equazione:
(formula 1.6)
Sostituendo mediante un altro semplice passaggio algebrico il valore della quota capitale così espressa, nella formula 1.4, il Debito residuo dopo il pagamento della rata k-esima, risulterà allora così determinato:
(formula 1.7)
Dalla 1.7 si verifica così una circostanza matematicamente inconfutabile: gli interessi pagati su ogni rata, vengono “capitalizzati” ovvero incorporati nel debito residuo risultante dopo il pagamento di ogni rata!
LA GENERAZIONE DI INTERESSI SU INTERESSI
A questo punto la generazione di “interessi sugli interessi” (cioè l’anatocismo) nei comuni piani di ammortamento, redatti in regime di interesse composto, è facilmente verificabile. Ci basta fare qualche semplice passaggio algebrico. A tal fine, dalla formula 1.7, possiamo dedurre che il debito residuo immediatamente prima del pagamento della Rata k-esima, risulta essere così formato:
(formula 1.8)
Ora, per dimostrare come nell’ammortamento francese (redatto in regime di interessi composti) esista anatocismo, non ci resta che sostituire nella formula 1.5, che descrive il calcolo della quota interessi, il valore del debito residuo utilizzato come base di calcolo degli interessi da corrispondere su ciascuna rata per andare a verificare che:
(formula 1.9)
Dalla formula 1.9 è possibile verificare la seguente, inconfutabile circostanza: nella base di calcolo degli interessi da corrispondere su ciascuna delle rate, sono sommati gli interessi già pagati sulla rata precedente e questo realizza proprio l’anatocismo.
MA QUINDI TUTTI I PIANI DI AMMORTAMENTO ALLA FRANCESE SONO “ANATOCISTICI”?
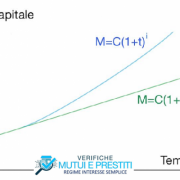
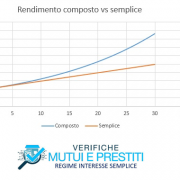
La risposta è NO. E’ possibile costruire piani di ammortamento in cui l’importo della rata sia determinato nel regime dell’interesse semplice anziché composto in tal modo depurando gli interessi da corrispondere su ciascuna rata da quelli derivanti dall’anatocismo.
Il problema infatti, è costituito dal modo in cui sono determinate le rate (cfr. la formula 1.1) e quindi le conseguenti quote capitali, debito residuo e quote interessi. Per una disamina approfondita di tali aspetti, si veda l’articolo di riferimento “Ammortamento francese e anatocismo“.
Scopri il nostro software per la verifica dell’anatocismo sul piano di ammortamento alla francese.
SOFTWARE UNICO NEL SUO GENERE IN ITALIA!
CALCOLA IL PIANO DI AMMORTAMENTO SIA
CON IL REGIME INTERESSE COMPOSTO
E SIA CON IL REGIME DI INTERESSE SEMPLICE

Dopo la laurea, frequenta con profitto il Master universitario di II livello in “Matematica per le Applicazioni” presso il Dipartimento di matematica dell’Università di Bologna
Dottore Commercialista e Revisore legale.
Consulente tecnico materia di contenzioso bancario
E’ iscritto nell’elenco dei Gestori della Crisi da Sovraindebitamento.
I NOSTRI SOFTWARE
Sub-domains
Your Text
Your Text
Your Text












 Benevento (BN)
Benevento (BN) +39 0824 317664
+39 0824 317664


































