Pubblicato il 13 settembre 2018
AMMORTAMENTO ALLA FRANCESE E ANATOCISMO
DOMANDA FONDAMENTALE:
Nell’ammortamento dei prestiti realizzato con la tecnica c.d “alla Francese”, esiste anatocismo?

PREMESSA E INQUADRAMENTO NORMATIVO
Una delle questioni più controverse nell’ambito del contenzioso bancario, è quella relativa alla presenza o meno, nei piani di ammortamento stilati con metodo c.d. “alla francese”, di anatocismo, ovvero di una capitalizzazione degli interessi sugli interessi che risulta nel nostro ordinamento generalmente vietata ex art. 1283 c.c.
L’articolo che segue, riprendendo anche quanto ampiamente discusso in un evento formativo tenuto presso l’ODCEC di Foggia il 10 maggio u.s. dallo scrivente insieme con il Prof. Antonio Annibali, (docente di matematica finanziaria f.r. presso l’Università La Sapienza di Roma), nasce da un’esigenza, che è poi anche una piccola ambizione, ovvero quella di contribuire a fare chiarezza su un argomento piuttosto controverso ed intorno al quale, al momento, pare esistere una confusione, ovvero una “disparità di vedute” – sia in Dottrina che Giurisprudenza – che appare per certi versi incomprensibile, data la natura di carattere fondamentalmente matematico della questione.
Sulla questione della presenza o meno di anatocismo insito nei comuni piani di ammortamento c.d. “alla francese” è infatti possibile trovare una pletora di pubblicazioni e pronunce giurisprudenziali che giungono a conclusioni contrastanti ed è opinione di chi scrive che, con ogni probabilità, neanche questo contributo servirà a dirimere ogni dubbio ma è lecito provarci.
Cominciamo quindi col rammentare che la capitalizzazione degli interessi è nel nostro ordinamento in generale vietata ex art. 1283 c.c. e risulta invece consentita da una deroga normativa posta dall’art. 120 – Decorrenza delle valute e calcolo degli interessi – del T.u.b. (D.lgs. n.385/93) come da ultimo modificato dal D.l. 14 febbraio 2016 n.18 ma per i soli conti correnti. Infatti il punto b) comma 2 della norma citata testualmente recita che:
“[…]gli interessi debitori maturati, ivi compresi quelli relativi a finanziamenti a valere su carte di credito, non possono produrre interessi ulteriori, salvo quelli di mora, e sono calcolati esclusivamente sulla sorte capitale[…]”
Con riferimento invece ai soli rapporti di conto corrente o di conto di pagamento, l’articolo in commento demanda le disposizioni ad apposita Delibera del CICR, che è stata emanata in data 3 agosto 2016.
Attualmente quindi permane, senza ordine di incertezza alcuna, un “divieto di capitalizzazione degli interessi corrispettivi” sulle operazioni di finanziamento diverse dall’apertura di credito in conto corrente, così come nella formulazioni precedenti della norma citata. Una eccezione è costituita dagli interessi di mora che si applicano sulle rate di rimborso scadute (e non pagate) di un finanziamento le quali, come noto, applicandosi su una rata costituita sia da capitale che da interessi, realizzano un anatocismo, ovvero una capitalizzazione degli interessi (di mora appunto) sugli interessi (corrispettivi insiti in ciascuna rata) che tuttavia risulta consentita dall’ordinamento.
Quanto sopra ci servirà quindi per fissare il postulato fondamentale, costituito dal divieto assoluto di capitalizzare gli interessi nelle operazioni di mutuo e prestiti a rimborso graduale in generale, su cui costruire tutto il ragionamento logico deduttivo necessario per arrivare alla risposta alla domanda che segue.
DOMANDA FONDAMENTALE: IL PIANO DI AMMORTAMENTO ALLA FRANCESE, REDATTO IN REGIME DI INTERESSE COMPOSTO, REALIZZA UNA CAPITALIZZAZIONE DEGLI INTERESSI SUGLI INTERESSI?
La lettura di questo articolo richiede un certo tempo ed una certa pazienza, tuttavia, per rispondere in maniera corretta e non arbitraria alla “domanda fondamentale”, bisogna innanzitutto approfondire la struttura tecnico attuariale di un piano di ammortamento, ovvero gli algoritmi di calcolo con cui sono costruite le rate di rimborso del prestito e successivamente verificare se tale tecnica realizzi o meno anatocismo, ovvero se le rate di rimborso del prestito così determinate incorporino o meno “interessi calcolati sugli interessi”.
Successivamente bisogna cercare di capire se, alla luce dei risultati – di per sé non discutibili perché inerenti il piano strettamente matematico finanziario – vi sia o meno una violazione delle norme sopra citate, ovvero se si realizzi o meno “anatocismo” in un siffatto piano di ammortamento ed in ogni caso se, pur in difetto di questo, i piani di ammortamento realizzati con siffatta tecnica contengano o meno un “costo occulto” non esplicitato in contratto attraverso la mera indicazione del tasso d’interesse applicato e del numero di rate di rimborso e del loro ammontare, ovvero se sussista o meno una violazione della normativa sulla trasparenza bancaria.
A tal fine, come ultimo passo, servirà dimostrare che esiste eventualmente un metodo di calcolo delle rate di rimborso alternativo a quello normalmente utilizzato dagli Intermediari finanziari e dallo stesso Stato (si pensi ai piani di rimborso delle obbligazioni tributarie proposti da Equitalia, oggi Agenzia per la Riscossione) che escluda l’anatocismo o che, in ogni caso, non incorpori un “costo occulto” per il debitore non esplicitato in contratto.
Si avverte fin d’ora il lettore che non è possibile comprendere tutto il filo logico delle argomentazioni qui svolte senza un adeguato approfondimento della parte di matematica finanziaria sottostante in quanto è questa – e solo questa – che fornisce i risultati obiettivi su cui fondare eventuali giudizi di merito, allo stesso modo in cui non è in alcun modo possibile giudicare sulla liceità o meno di una sostanza chimica, senza una approfondita conoscenza della sua struttura chimica molecolare (e quindi di chimica).
Ci rendiamo conto che tale circostanza può essere in alcuni casi di impedimento per il lettore che non possieda un particolare feeling con l’analisi matematica e la matematica finanziaria in particolare ma in tal caso sarebbe opportuno astenersi da giudizi in merito, ovvero rispondere “non lo so” alla domanda sopra posta, piuttosto che rispondere con un “Si” o un “No” fondati su mere congetture, perché fin quando la risposta resta nell’ambito della sfera privata nessun problema si pone ma quando si viene incaricati di rispondere a tale domanda nell’ambito di un procedimento giudiziario, in veste di Organo giudicante o di Consulente Tecnico d’Ufficio, ovvero in qualità di “pubblico ufficiale”, allora il reato di “falso ideologico” di cui agli art.479 e ss. del cod. pen. è dietro l’angolo.
DEFINIRE L’EQUIVALENZA FINANZIARIA TRA IMPORTI DIVERSI DISPONIBILI IN EPOCHE DIVERSE. LE OPERAZIONI DI CAPITALIZZAZIONE E ATTUALIZZAZIONE: I REGIMI FINANZIARI
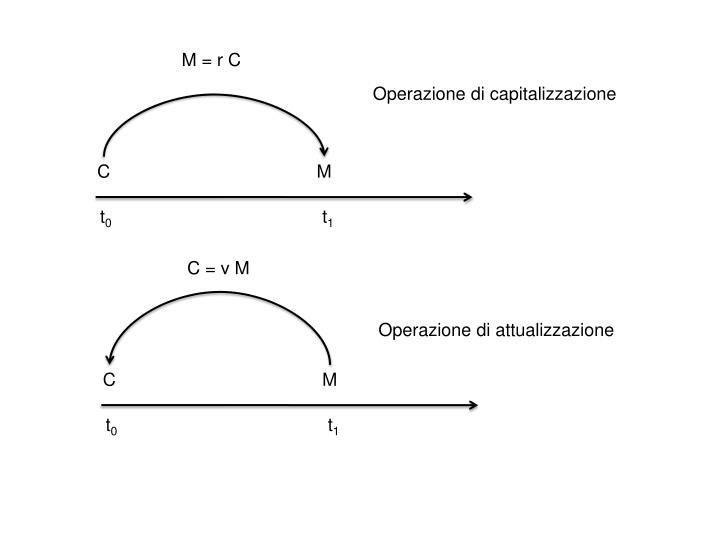
La matematica finanziaria, senza la conoscenza della quale chiunque tenti di rispondere alla domanda fondamentale commette un sostanziale arbitrio intellettuale, così come d’altra parte farebbe chiunque volesse stabilire se l’accelerazione di un corpo in movimento in un determinato sistema di riferimento sia costante o meno senza conoscere le leggi della fisica, ha lo scopo principale di stabilire l’equivalenza finanziaria di importi diversi, disponibili in epoche diverse e lo fa definendo due principali operazioni: l’operazione di capitalizzazione e l’operazione di attualizzazione.
A tal fine si parte dalla definizione dei concetti elementari di capitale, interesse e tasso d’interesse e si finisce con il definire delle “leggi matematiche”, ovvero dei modelli matematici che descrivono il processo di “generazione degli interessi” e del correlato processo di “accumulazione di capitale” in maniera del tutto analoga alle leggi della fisica che descrivono lo spostamento di un corpo nel tempo: il fatto che leggi della fisica siano dipendenti da “fenomeni reali” mentre quelle della matematica finanziaria da “fenomeni artificiali” ovvero creati (immaginati per meglio dire) dall’uomo, secondo quelle che sono “convenzioni sociali” codificate poi in norme di legge, non cambia la sostanza delle cose: senza la conoscenza dei modelli matematici che descrivono i fenomeni oggetto d’indagine e ne definiscono il comportamento, bisognerebbe astenersi dal giudicare.
Nella valutazione di una operazione finanziaria assume particolare rilievo la necessità di determinare, per il debitore, il costo del finanziamento (che per il creditore rappresenterà specularmente il guadagno) sia in termini assoluti che relativi (percentuali). A tal proposito valgono le seguenti definizioni.
1. Interesse. Data una somma C (capitale) ottenuta in prestito ed una somma M (montante) da restituire alla scadenza, T risulta in genere M>C. Si definisce allora interesse la differenza seguente:
I=M-C
(1.0)
2. Tasso d’interesse. Per permettere di effettuare confronti tra importi (C ed M) di diverso ammontare, si definisce il tasso d’interesse, costituito dal rapporto tra l’ammontare totale degli interessi da corrispondere ed il capitale ottenuto in prestito:
i=\frac{M-C} C=\frac I C
(1.1)
3. Tasso d’interesse effettivo periodale. Generalmente la restituzione del capitale C maggiorato degli interessi, ovvero la corresponsione di M, avviene in un’epoca tn diversa da quella in cui si ottiene il prestito, tk, con tn > tk . Il numero fornito dalla (1.1) quando riferito esplicitamente al periodo tn – tk prende il nome di tasso d’interesse effettivo periodale.
Il numero i(tk, tn) rappresenta allora il tasso d’interesse effettivo prodotto da ogni unità di capitale investito c, tra le epoche tk e tn
Per convenzione e per permettere il confronto tra operazioni di diverso ammontare attuate in epoche diverse, il tasso d’interesse effettivo è riferito in genere all’anno (tasso d’interesse effettivo annuo) o a frazioni intere dello stesso (semestre, trimestre, bimestre, mese).
- Con l’operazione di capitalizzazione, dato un certo capitale C, disponibile in t_0 ed impiegato per un certo periodo di tempo ad un certo tasso d’interesse, si vuole stabilire qual è l’importo, detto Montante ed in indicato con M, disponibile all’epoca t1 > t0 , che risulta finanziariamente equivalente al capitale C. A tal fine si definisce una funzione matematica che si suole indicare con la lettera “r” e prende il nome di “funzione fattore di capitalizzazione”. Tale funzione deve godere di alcune proprietà matematiche che vedremo più avanti.
- Con l’operazione di attualizzazione si esegue l’operazione inversa, ovvero noto un certo importo M, disponibile in t1, si vuole conoscere qual è il valore del Capitale C, da impiegare nel periodo t1 – t0 ad un certo tasso d’interesse i, che genererà l’importo M. A tal fine si definisce una funzione matematica che si suole indicare con la lettera “v”, che è l’inversa di r e prende il nome di “funzione fattore di attualizzazione”: anche tale funzione deve godere di alcune proprietà matematiche che vedremo più avanti.
Spesso ci si concentra sul fenomeno della capitalizzazione degli interessi, ovvero conoscere il valore futuro M (il montante), ad una certa epoca tn, di una certa somma C (il capitale) impiegata ad un certo tasso i per un certo periodo Tn – t0 dimenticando che specularmente in finanza si pone il problema inverso, ovvero conoscere il valore attuale, cioè in t0
o in una epoca qualsiasi t0 < t k-1< tk . . < tn di una certa somma disponibile ad una epoca tn > t k-1> tk . . < t0 e che tali operazioni devono essere “reversibili”, ovvero deve essere sempre possibile, noto il tasso d’interesse ed i tempi di valutazione, conoscere C a partire da M e viceversa.
Vedremo adesso come per definire correttamente l’equivalenza finanziaria di cui sopra è necessario ed imprescindibile specificare matematicamente il regime finanziario in cui si compiono le valutazioni, altrimenti le operazioni di capitalizzazione ed attualizzazione non saranno reversibili.
- Fattore di capitalizzazione e montante. E’ di fondamentale importanza definire quindi le regole matematiche attraverso cui avviene l’incremento del capitale C al tasso i( tk, tn ) nel periodo tn – tk . Tale incremento avviene infatti secondo delle regole precise che, matematicamente parlando, è possibile esplicitare attraverso una funzione chiamata “fattore di capitalizzazione”, (o fattore di montante) definita attraverso il seguente schema:
i\left(t_k,t_n\right)=\frac{M-C} C=\frac M C-1=r\left(t_k,t_n\right)-1
(1.2)
Dalla (1.2) è possibile quindi esplicitare la seguente relazione:
r\left(t_k,t_n\right)=1+i\left(t_k,t_n\right)
(1.3)
La 1.3 definisce in generale una “legge di capitalizzazione” o la “funzione fattore di capitalizzazione” o “fattore di montante”. Sicché, risulta che il capitale C s’incrementa nel periodo tn – tk secondo la seguente legge:
M=C\cdot\left(t_k,t_n\right)
(1.4)
2. Fattore di sconto e valore attuale. A partire dalla 1.4 è possibile risolvere il problema inverso, ovvero conoscere il valore del capitale C, che, impiegato all’epoca t0 al tasso i ha generato il montante M all’epoca tk. In tal caso si definisce quindi il valore attuale di M (che all’epoca tk è pari a C), attraverso la seguente relazione:
C=M\frac1{r\left(t_n,t_k\right)}
(1.5)
Specularmente alla 1.3 si definisce quindi la funzione fattore di sconto, che attraverso la 1.5 risulta definita dalla seguente relazione:
v\left(t_k,t_n\right)=\frac 1{r\left(t_n,t_k\right)}=\frac1{1+i\left(t_k,t_n\right)}
(1.6)
Definite le funzioni fattori di capitalizzazione (1.4) e fattori di sconto (1.6) a livello generale, resta ora da esplicitarne le principali proprietà matematiche. In generale esistono numerose funzioni definibili attraverso le 1.3 ed 1.6. Ogni classe di funzioni così definita prende il nome di regime di capitalizzazione. Per una disamina di queste problematiche, si rimanda ad una qualsiasi testo di matematica finanziaria almeno di livello universitario. Per ciò che qui interessa invece, si analizzeranno i due “regimi di capitalizzazione”, più utilizzati nella pratica finanziaria e commerciale: il regime d’interesse composto (RIC) ed il regime dell’interesse semplice (RIS).
3. Regime dell’interesse semplice Si ipotizzi che, su una determinata somma prestata C, vengano periodicamente corrisposti degli interessi senza però che questi ultimi vengano a loro volta re-investiti nel periodo di tempo t = tn – tk. In tal caso avremo definito una legge di capitalizzazione detta “regime dell’interesse semplice”, ovvero una funzione 1.3 così definita:
r\left(t_k,t_n\right)=1+i\left(t_k,t_n\right)=1+i(t)
(1.7)
4. Regime dell’interesse composto. Si ipotizzi ora una serie di scadenze intermedie tk+τ con t0 < t k-1 < t k … < t n e si ipotizzi che gli interessi via via corrispondenti per ogni scadenza vengano a loro volta re-investiti al medesimo tasso i ( tk, tn ) per cui si avrà una successione definita nel modo seguente:
r\left(t_k,t_n\right)=\left(1+i\left(t_k,t_{k+\tau }\right)\right){\cdot}\left(1+i\left(t_{k+\tau },t_n\right)\right)=\left(1{\text ~}+i\left(t_k,t_n\right)\right)^{t_n-t_k}
(1.8)
Si noti che, ponendo tn – tk = t, la 1.8 si può riscrivere come:
r\left(t\right)=\left(1{\text ~}+i\left(t\right)\right)^t
(1.9)
ed in tal caso è evidente che essa coincide con la 1.7 solo per periodi unitari, ovvero per t = 1 mentre in generale, per t >1, risulta:
(1+ i(t))^{t} >( {1 + i(t)} )
(1.10)
Si noti come quella indicata in 1.10 è la funzione di capitalizzazione. La corrispondente funzione valore attuale risulta essere:
{v( t) =( {1 + i( t)} )^{-t}}
(1.11)
La funzione valore attuale nel RIS è invece la seguente:
v(t)=\frac 1{r(t)}=\frac1{1+t{\cdot}i(t)}
(1.12)
Si noti come anche i valori delle funzioni 1.11 – 1.12 coincidano per t = 1 mentre in generale per t >1, risulta:
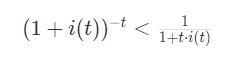
(1.13)
Come sarà chiaro nella sezione successiva quando parleremo dei regimi d’interesse, la scelta di una forma funzionale piuttosto che un’altra per il fattore di capitalizzazione (ed il correlato fattore di sconto) influenza in maniera decisiva i risultati dei calcoli relativi agli interessi da corrispondere in una operazione di finanziamento (ed ovviamente nella redazione di un piano di ammortamento).
REGIMI D’INTERESSE E ANATOCISMO
A questo punto siamo in grado di stabilire in che misura, a parità di tasso d’interesse i, la scelta di un regime finanziario piuttosto che un altro abbia effetto sulla determinazione finale degli interessi complessivamente dovuti in un operazione di finanziamento.
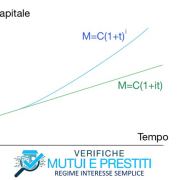
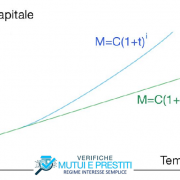
Come già matematicamente evidente dalla formula (1.8), il regime dell’interesse composto realizza una capitalizzazione continua degli interessi e quindi l’anatocismo. La ragione è che, per costruzione, nel regime degli interessi composto si ipotizza che gli interessi man mano prodotti vengano istantaneamente reinvestiti.
Nel regime di interesse semplice invece, gli interessi via via prodotti vengono tenuti sempre distinti dal capitale e non generano altri interessi.
Questo risultato è evidente dalla tabella e dal grafico sotto riportati, dove si sono calcolati gli interessi maturati su un capitale di €100.000 al tasso annuo nominale del 10,00% in 20 anni:
Tabella 1: esempio di calcolo del montante nel RIC e nel RIS
|
Tempo in anni |
Tasso d’interesse |
Montante maturato in RIC |
Montante maturato in RIS |
|
0 |
10,00% |
100.000,00 |
100.000,00 |
|
1 |
10,00% |
110.000,00 |
110.000,00 |
|
2 |
10,00% |
121.000,00 |
120.000,00 |
|
3 |
10,00% |
133.100,00 |
130.000,00 |
|
4 |
10,00% |
146.410,00 |
140.000,00 |
|
5 |
10,00% |
161.051,00 |
150.000,00 |
|
6 |
10,00% |
177.156,10 |
160.000,00 |
|
7 |
10,00% |
194.871,71 |
170.000,00 |
|
8 |
10,00% |
214.358,88 |
180.000,00 |
|
9 |
10,00% |
235.794,77 |
190.000,00 |
|
10 |
10,00% |
259.374,25 |
200.000,00 |
|
11 |
10,00% |
285.311,67 |
210.000,00 |
|
12 |
10,00% |
313.842,84 |
220.000,00 |
|
13 |
10,00% |
345.227,12 |
230.000,00 |
|
14 |
10,00% |
379.749,83 |
240.000,00 |
|
15 |
10,00% |
417.724,82 |
250.000,00 |
|
16 |
10,00% |
459.497,30 |
260.000,00 |
|
17 |
10,00% |
505.447,03 |
270.000,00 |
|
18 |
10,00% |
555.991,73 |
280.000,00 |
|
19 |
10,00% |
611.590,90 |
290.000,00 |
|
20 |
10,00% |
672.749,99 |
300.000,00 |
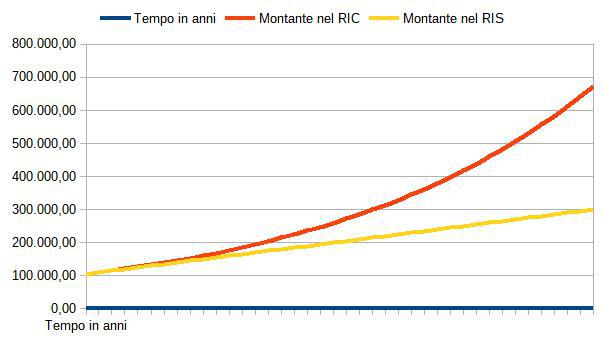
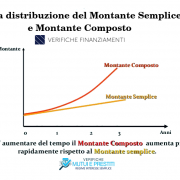
Come si vede dalla tabella sopra riportata, nello stesso arco temporale (20 anni), il montante (capitale e interessi) calcolato secondo il regime composto è più che doppio rispetto agli interessi calcolati in regime semplice: nel regime dell’interesse composto infatti, gli interessi complessivamente dovuti crescono in maniera esponenziale, mentre nel regime dell’interesse semplice si ha una crescita lineare rispetto al tempo, come evidente dal grafico sottostante (Grafico 1).
Per ragioni che saranno chiare quando si tenterà di spiegare in che modo è possibile costruire dei piani di ammortamento a rata costante, è indispensabile studiare anche le funzioni fattore di sconto, necessarie per risolvere il problema inverso, ovvero il problema della “attualizzazione di una somma di denaro”: data cioè una certa somma di denaro disponibile ad una certa data, vogliamo conoscere il capitale che, impiegato ad un certo tasso nel lasso di tempo considerato, l’ha generata.
Supponiamo quindi di voler sapere qual è il capitale da investire, al tasso del 10% annuo, per ottenere il montante M=100.000,00: quello che stiamo cercando è quindi il “valore attuale” di €100.000 e da quanto sopra il lettore accorto intuisce che il suo valore differisce a seconda del regime finanziario che si decide di utilizzare per fare i calcoli.
A tal fine nella tabella che segue si utilizzeranno quindi le due funzioni 1.11 e 1.12, ovvero le funzioni fattore di sconto rispettivamente nel RIS e nel RIC: come ci si aspetta, le somme da impiegare anno per anno, a parità di tasso, saranno più basse nel caso in cui i calcoli vengano eseguiti con il RIC piuttosto che con il RIS
Tabella 2: esempio di calcolo del valore attuale nel RIC e nel RIS
|
Tempo in anni |
Tasso d’interesse |
Valore attuale nel RIC |
Valore attuale nel RIS |
|
0 |
10,00% |
100.000,00 |
100.000,00 |
|
1 |
10,00% |
90.909,09 |
90.909,09 |
|
2 |
10,00% |
82.644,63 |
83.333,33 |
|
3 |
10,00% |
75.131,48 |
76.923,08 |
|
4 |
10,00% |
68.301,35 |
71.428,57 |
|
5 |
10,00% |
62.092,13 |
66.666,67 |
|
6 |
10,00% |
56.447,39 |
62.500,00 |
|
7 |
10,00% |
51.315,81 |
58.823,53 |
|
8 |
10,00% |
46.650,74 |
55.555,56 |
|
9 |
10,00% |
42.409,76 |
52.631,58 |
|
10 |
10,00% |
38.554,33 |
50.000,00 |
|
11 |
10,00% |
35.049,39 |
47.619,05 |
|
12 |
10,00% |
31.863,08 |
45.454,55 |
|
13 |
10,00% |
28.966,44 |
43.478,26 |
|
14 |
10,00% |
26.333,13 |
41.666,67 |
|
15 |
10,00% |
23.939,20 |
40.000,00 |
|
16 |
10,00% |
21.762,91 |
38.461,54 |
|
17 |
10,00% |
19.784,47 |
37.037,04 |
|
18 |
10,00% |
17.985,88 |
35.714,29 |
|
19 |
10,00% |
16.350,80 |
34.482,76 |
|
20 |
10,00% |
14.864,36 |
33.333,33 |
Dalla Tabella 2 sopra riportata si evince come, a parità di tasso d’interesse annuo nominale, il valore delle somme da impiegare per ottenere la somma finale (il montante) di €100.000,00 in 20 anni, è inferiore nel RIC rispetto al RIS, a parte il primo anno, per cui i due valori coincidono.
Questo fatto può esprimersi in termini più tecnici affermando che il valore attuale delle somme impiegate nel RIC è sempre più basso rispetto al valore attuale delle somme impiegate nel RIS, come si vede meglio anche dal grafico sotto riportato di confronto delle due funzioni valore attuale, rispettivamente nel RIC (formula 1.11) e nel RIS (formula 1.12).
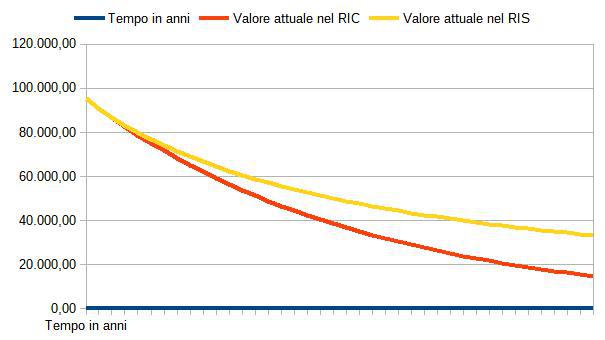
I risultati di cui sopra devono essere tenuti bene a mente in quanto la chiave di risposta alla domanda principale è insita proprio in questi risultati, ignorando i quali non si possono che affermare delle memorabili sciocchezze in merito.
__________________________________________________________________________
STRUTTURA DI UN PIANO DI AMMORTAMENTO: DEFINIZIONI FONDAMENTALI
In questa parte considereremo il concetto di “prestito” o di “mutuo” e del conseguente piano di rimborso (c.d. “ammortamento”) da un punto di vista squisitamente matematico, tralasciando quindi le correlate definizioni giuridiche.
L’insieme delle specifiche relative ai tempi di rimborso del capitale e al pagamento degli interessi si chiama il piano di rimborso o di ammortamento del prestito. Considerando la situazione standard, lo schema e la terminologia classici sono i seguenti:
-Un primo soggetto presta ad un secondo soggetto un ammontare di capitale, che indicheremo con S, concordando le modalità di ammortamento del prestito.
-L’ammortamento avverrà tramite rate (o annualità) Rk, rispettivamente in scadenza ai tempi k = 1, 2, . . . , n.
-Ogni rata Rk si decomporrà in due diverse quote: Rk = Ck + Ik, rispettivamente dette quote capitale (Ck) e quote interessi (Ik).
-Alla fine del k-esimo anno, viene calcolato il debito ancora da rimborsare negli anni successivi, il cosiddetto debito residuo (Dk). Ad ogni pagamento di quota capitale Ck, il debito residuo decresce secondo la relazione di ricorrenza:
Dk = Dk−1 − Ck
–Alla fine del k-esimo anno, si calcola il debito gi`a pagato, il cosiddetto debito estinto (Ek). Ad ogni pagamento di quota capitale Ck, il debito estinto cresce secondo la relazione di ricorrenza:
Ek = Ek−1 + Ck
Si definisce allora mutuo una operazione finanziaria conforme allo schema seguente.
1. All’epoca t0 un soggetto (mutuante o creditore) cede ad un secondo soggetto (mutuatario o debitore) un importo S (importo del mutuo o prestito), che viene frazionato negli importi non negativi
C1,C2,.....Cn, (quote capitale), corrisposti alle scadenze t0,t1,.....tn,in maniera tale che (condizione di chiusura):
\overset{n}{\underset{k=1}{\sum }}C_k=S
(2.0)
2. Attraverso le quote capitale si definisce il debito residuo Dk all’epoca tk,
D0=S; Dk = Dk-1 – Ck ( k = 1, …,n )
ovvero
D_k=S-\overset k{\underset{i=1}{\sum }}C_i
(2.1)
La quantità: Ek = S – D k , è detta “debito estinto” all’epoca tk . Evidentemente, dalla (2.0) e dalla (2.1) discendono le relazioni: Dn = 0 e Ek = S
3. Sulla somma ottenuta in prestito il mutuatario deve corrispondere degli interessi, maturati per ogni scadenza sul debito residuo ad un determinato tasso i che per convenzione viene espresso in ragione d’anno e che per tale ragione è detto anche TAN (tasso annuo nominale). Per pagamenti frazionati rispetto all’anno (semestrali, trimestrali, mensili etc.) il tasso d’interesse da prendere in considerazione per il calcolo degli interessi diviene allora pari ad:
i_k=i{\cdot}\frac 1 m
(2.2)
dove m indica il numero di periodi in cui è suddiviso l’anno, per cui, in caso di pagamento semestrale, si avrà m=2, per pagamenti mensili m=12, etc.
Ciò comporta che, ad ogni scadenza, tk il mutuatario debba adempiere due distinte ma correlate obbligazioni, versando al mutuante:
-
-
la k-esima quota di capitale Ck ;
-
la k-esima quota interessi, Ik che riguarda gli interessi maturati sul debito residuo al tasso d’interesse tk-1 tra le due epoche tk-1 e tk .
-
4. Pertanto, ad ogni epoca tk il debitore deve corrispondere al creditore un importo Rk detto “rata di ammortamento” e pari alla somma delle due componenti come sopra determinate, ovvero:
R_k=C_k+I_k
(2.3)
Dove ogni quota interessi risulterà calcolata nel seguente modo:
I_k=D_{k-1}{\cdot}i\left(t_{k-1},t_k\right)
(2.4)
OSSERVAZIONI AL CALCOLO DELLA RATA IN UN MUTUO: LA SPECIFICAZIONE DEL REGIME DI INTERESSE
Si noti a questo punto una cosa: le formule fin qui elencate per descrivere la struttura fondamentale di un piano di ammortamento, non sono assolutamente sufficienti per calcolare una rata di importo costante, definita attraverso la formula 2.3 e che realizzi anche la “condizione di chiusura semplice” esplicitata dalla formula 2.0.
La ragione è nel fatto che, dal momento che con il pagamento di ogni rata intendiamo pagare sia il capitale che gli interessi, per definire in maniera univoca e corretta l’importo della rata che stiamo cercando, è necessario specificare quale forma funzionale stiamo adottando per la determinazione dei fattori di sconto vk da applicare a ciascuna rata, affinché il loro valore attuale sia esattamente pari al capitale ricevuto in prestito.
In altre parole: per definire in maniera univoca l’importo delle rata costante che soddisfi la condizione di chiusura finale, è necessario specificare la scelta del regime degli interessi da adottare.
E’ questo il fulcro del ragionamento da seguire per rispondere in maniera corretta alla “domanda fondamentale”.
A tal fine, e per quel che qui interessa, bisogna sapere che si può utilizzare sia il regime degli interessi composto, che il regime degli interessi semplice, ovvero si può utilizzare come fattore di sconto una delle due forme funzionali definite rispettivamente dalla 1.11 o dalla 1.12.
Il risultato cambia in maniera notevole: come intuibile dai risultati già visti sopra quando abbiamo brevemente illustrato i regimi di interesse, la rata di ammortamento calcolata applicando il regime degli interessi composto sarà notevolmente più alta della rata calcolata applicando il regime degli interessi semplice.
Per eseguire detto calcolo, è necessario andare avanti nella trattazione matematica della questione introducendo il concetto di “rendita finanziaria“.
IL CALCOLO DELLA RATA: IL PIANO DI AMMORTAMENTO COME RENDITA FINANZIARIA
Per costruire il nostro piano di ammortamento e rispondere in maniera corretta alla “domanda fondamentale”, a questo è necessario andare avanti nella trattazione matematica introducendo il concetto di “rendita finanziaria“, necessario per calcolare l’importo della rata che restituisca il capitale e gli interessi attraverso una serie di pagamenti equi-intervallati nel tempo.
Dal punto di vista matematico, il problema da risolvere è come calcolare una serie ordinata di pagamenti (incassi per il mutuante) di ammontare {R1 , R 2, …, Rk ,…, Rn }da corrispondere alle scadenze {t1 , t 2, …, tk ,…, tn } a fronte di un incasso inziale (erogazione del credito per il mutuante) iniziale, in genere indicato con S, che è l’ammontare del prestito.
La trattazione matematica delle rendite, può svolgersi sia nel regime dell’interesse composto che nel regime dell’interesse semplice. Ciò che in particolare interessa è definire il montante di una rendita ed il valore attuale della stessa. E’ chiaro che i risultati saranno influenzati dal regime di interesse che si sceglie, dal momento che cambiano le forme funzionali rispettivamente della funzione fattore di montante e della funzione fattore di sconto.
Per brevità di trattazione nonché per gli scopi del presente articolo, ci limiteremo ad enunciare i risultati relativi alle rendite nel regime dell’interese composto.
Rimandiamo il lettore interessato ai testi citati in bibliografia per gli approfondimenti e le relative dimostrazioni matematiche (che si fondano sui concetti di successioni e serie).
RENDITE FINANZIARIE NEL REGIME DELL’INTERESSE COMPOSTO
Si definisce “montante di una rendita“, e si indica con S, la somma dei montanti delle singole rate costituenti la rendita. Nel regime composto tale valore è definito utilizzando la funzione fattore di montante esplicitata in 1.8, per cui, il valore che stiamo cercando, è dato dalla formula seguente:
S=\overset n{\underset{k=1}{\sum }}R_k(1+i)^{n-k}
(2.5)
Supponendo adesso che il valore della rata sia costante e fissato pari ad 1, è possibile ridurre la successione di importi in 2.5 attraverso la seguente formulazione:
\overset n{\underset{k=1}{\sum }}(1+i)^{n-k}=\overset {n-1}{\underset{k=o}{\sum }}r^{k}=\frac{(1+i)^n-1} i=S_{n\neg i}
(2.6)
In maniera analoga si definisce il valore attuale di una rendita unitaria intera come:
\overset n{\underset{k=1}{\sum }}(1+i)^{-k}=\overset n{\underset{k=1}{\sum }}v_k=\frac{1-(1+i)^{-n}} i=a_{n\neg i}
(2.7)
A questo punto siamo finalmente in grado di definire l’importo della nostra rata costante. A tal fine, cominciamo riscriviamo la “condizione di chiusura” già esplicitata in 2.0 per includere nel calcolo oltre alle quote capitali, anche gli interessi che vogliamo corrispondere su ciascuna rata.
Ciò si fa imponendo la condizione che “la somma dei valori attuali delle rate sia pari esattamente al capitale prestato“.
In tal modo si ottiene quindi la seguente nuova “condizione di chiusura” (o di eliquilibrio) del piano di ammortamento:
S=\overset n{\underset{k=1}{\sum }}R_k(1+i)^{-k}=\overset n{\underset{k=1}{\sum }}R_kv^k
(2.8)
La “condizione di chiusura”, sopra definita si realizza in pratica moltiplicando ogni rata per il fattore di sconto corrispondente alla sua scadenza e poi sommando tutti i valori attuali delle rate così ottenuti.
A questo punto per ottenere l’importo della nostra rata costante, necessario per restituire interamente il capitale preso a prestito (che indicheremo con C) più gli interessi, ci basta sostituire nella 2.8 il valore trovato nella 2.7 così ottenendo:
R=\frac C{a_{n\neg i}}=C{\cdot}\frac i{1-v^n}=\frac{\left(1+i\right)^n}{\left(1+i\right)^n-1}{\cdot}i{\cdot}C=\left(1+\frac 1{\left(1+i\right)^n-1}\right){\cdot}i{\cdot}C
(2.9)
A questo punto possiamo esplicitare le altre grandezze del nostro piano di ammortamento in forma chiusa. In particolare, il debitore residuo all’epoca k-esima sarà pari a:
D_k=R{\cdot}\overset n{\underset{j=k+1}{\sum }}v^{j-k}=S{\cdot}\frac i{1-v^n}{\cdot}\frac{1-v^{n-k}} i=S{\cdot}\frac{1-v^{n-k}}{1-v^n}
(2.10)
Lo schema generale di un piano di ammortamento alla francese a rata costante, redatto in regime di interessi composti, risulta quindi essere il seguente:
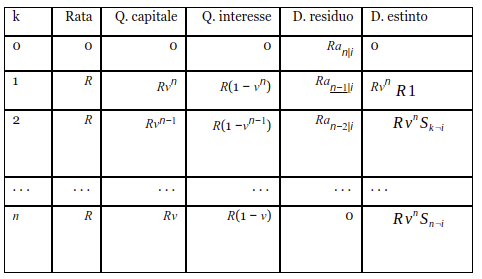
Soffermiamo adesso l’attenzione sulla 2.9 (calcolo della rata) con tutti i suoi passaggi intermedi, nonché sullo schema di calcolo sopra riportato: è evidente come per la determinazione della rata venga utlizzata la funzione fattore di montante esponenziale (1.10) e che per la successiva determinzione di ogni quota capitale, e quindi per la determinazione del debito residuo ad ogni scadenza, venga utilizzata la funzione fattore di sconto del regime degli interessi composto (definita in 1.11).
Già da questa formulazione, chi si interessa di analisi funzionale potrà rispondere alla domanda fondamentale dal momento che, come risulta chiaro, il presuspposto con cui viene determinata ogni quota del debito residuo è che tra un’epoca e l’altra siano incorporati (i.e. “capitalizzazti”) nel calcolo gli interessi già corrisposti, come sarà meglio chiarito (e definitivamente dimostrato) nelle sezioni successive.
PIANO DI AMMORTAMENTO ALLA FRANCESE NEL REGIME DEGLI INTERESSI COMPOSTO: BREVE VERIFICA MATEMATICA DELL’ANATOCISMO
Adesso abbiamo tutti gli strumenti per poter rispondere correttamente alla domanda fondamentale, senza fuorvianti ed eccessive semplificazioni o congetture.
Per ciò che qui interessa, partiremo quindi dalla formula 2.4 dalla quale è evidente come la quota di interessi corrispettivi da corrispondere su ciascuna rata di rimborso del prestito sia determinata dalla misura del tasso di interesse ik in vigore tra le due scadenze successive tk-1 e tk e dal debito residuo immediatamente precedente, ovvero dal debito residuo in tk-1 e risultante dopo il pagamento della rata immediatamente precedente, cioè Dk-1. E’ quindi necessario, per rispondere alla domanda fondamentale, capire come si forma il debito residuo alla fine di ciascun pagamento. A tal fine, dalla 2.1 sappiamo che, per ogni rata k, vale la relazione:
D_k=D_{k-1}-C_k
(3.0)
Si faccia ora la massima attenzione ad una cosa: dalla 2.3 risulta evidentemente:
C_k=R_k-I_k
(3.1)
Ora: sostituendo nella formula 3.0 il valore di Ck determinato attraverso la 3.1, si verifica banalmente che:
D_k=D_{k-1}-R_k+I_k
(3.2)
Adesso, ragioniamo su come viene calcolata la quota interessi (formula 2.4). Tutto quello che dobbiamo fare è, servendoci della 2.8, andare a vedere come in realtà viene calcolata la quota di debito residuo Dk-1 sulla quale viene calcolata la quota interessi Ik e verificare se essa viene o meno calcolata anche sugli interessi pregressi, ovvero se esista o meno anatocismo.
Dalla 3.2, con opportuno cambio notazionale, possiamo scrivere:
D_{k-1}=D_{k-2}-R_{k-1}+I_{k-1}
(3.4)
A questo punto, per portare a termine la nostra dimostrazione, non ci resta che sostituire il valore di Dk-1 come esplicitato nella 3.3 all’interno della formula di calcolo della quota interessi da corrispondere su ciascuna rata, determinata attraverso la 2.4.
I_k=(D_{k-2}-R_{k-1}+I_{k-1}){\cdot}i\left(t_{k-1},t_k\right)
(3.5)
Leggendo con attenzione la 3.5 è evidente una circostanza che non è in alcun modo confutabile: nella base di calcolo per la determinazione delle quote interessi Ik, da corrispondere su ciascuna rata Rk, ovvero nel debito residuo risultante dopo il pagamento di ogni rata, vengono sommati gli interessi Ik-1 già corrisposti sulla rata precedente Rk-1.
In altre parole: gli interessi corrisposti su ciascuna rata vengono “capitalizzati” e questo realizza proprio l’anatocismo.
Si noti che la verifica di cui sopra è banale e vale per qualsiasi piano di ammortamento, redatto in regime di interesse composto: francese, italiano etc.
E’ possibile dimostrare – ma tale dimostrazione esula dagli scopi di questo articolo – come utilizzando opportune tecniche atturiali sia possibile eliminare “l’effetto anatocistico” nel piano di ammortamento a rata costante.
Questo avviene utilizzando il regime degll’interesse semplice anziché composto e quindi utilizzando una diversa forma funzionale per i fattori di attualizzazione con cui si determina l’importo della rata (cfr la 2.8). In un prossimo articolo daremo tale dimostrazione.
Per ciò che qui interessa possiamo quindi rispondere alla “domanda fondamentale” nel seguente modo:
al contrario di quanto affermato da molti, che per rispondere alla “domanda fondamentale” si limitano alla verifica della 2.4, “nella struttura matematico-attuariale di un piano di ammortamento alla francese redatto in regime di interessi composti non c’è assolutamente nulla che possa evitare la generazione di interessi composti e quindi l’anatocismo!“
Questo fatto, che è un fatto e non un’opinione, risulta evidente dalla tabella e dal grafico successivi in cui è mostrato l’andamento della funzione Rata, come escplicitata nella formula 2.9, al crescere del tasso d’interesse.
A tal fine immaginiamo di avere un finanziamento di €100.000 da restituire in 20 anni mediante il pagamento di 240 rate mensili posticipate: è evidente l’andamento “esponenziale” dell’importo della rata al crescere del tasso d’interesse. Il grafico 3 mostra infatti l’andamento tipico di una funzione esponenziale (cfr. Grafico 1). Questo è dovuto proprio al fenomeno anatocistico insito in tali piani di ammortamento.
Tabella 3: variazione della rata di ammortamento in un piano di ammortamento alla francese redatto in regime di interessi composti funzione del tasso d’iteresse
| TAN (tasso annuo nominale) | Importo rata nel RIC |
| 1,000% | € 459,89 |
| 2,000% | € 505,88 |
| 3,000% | € 554,60 |
| 4,000% | € 605,98 |
| 5,000% | € 659,96 |
| 6,000% | € 716,43 |
| 7,000% | € 775,30 |
| 8,000% | € 836,44 |
| 9,000% | € 899,73 |
| 10,000% | € 965,02 |
| 11,000% | € 1.032,19 |
| 12,000% | € 1.101,09 |
| 13,000% | € 1.171,58 |
| 14,000% | € 1.243,52 |
| 15,000% | € 1.316,79 |
| 16,000% | € 1.391,26 |
| 17,000% | € 1.466,80 |
| 18,000% | € 1.543,31 |
| 19,000% | € 1.620,68 |
| 20,000% | € 1.698,82 |
| 21,000% | € 1.777,64 |
| 22,000% | € 1.857,06 |
| 23,000% | € 1.937,00 |
| 24,000% | € 2.017,41 |
| 25,000% | € 2.098,22 |
| 26,000% | € 2.179,38 |
| 27,000% | € 2.260,84 |
| 28,000% | € 2.342,57 |
| 29,000% | € 2.424,53 |
| 30,000% | € 2.506,69 |
| 31,000% | € 2.589,02 |
| 32,000% | € 2.671,49 |
| 33,000% | € 2.754,10 |
| 34,000% | € 2.836,81 |
| 35,000% | € 2.919,61 |
Grafico 3: andamento della Rata di ammortamento nell’ammortamento francese (in regime di interessi composti) al variare del tasso d’interesse
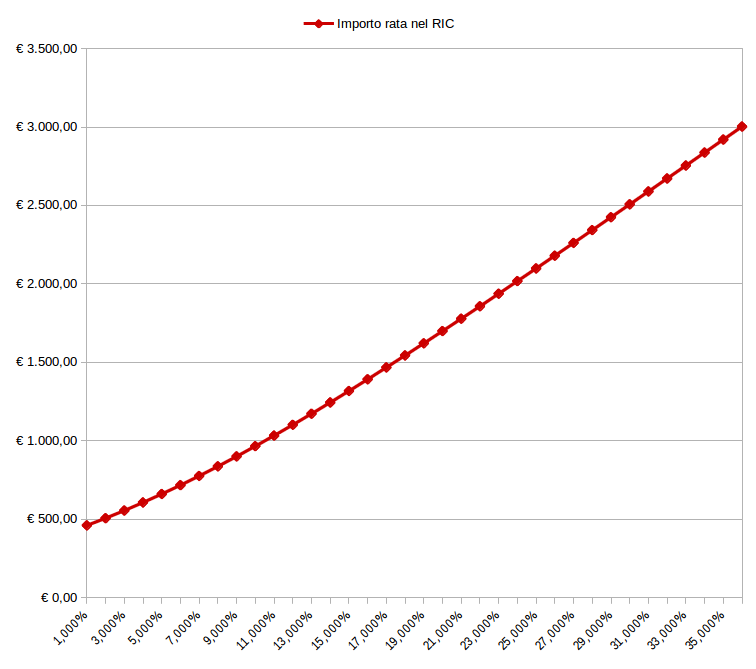
Dal grafico sopra è evidente l’andamento esponenziale tipico della funzione fattore di montante nel RIC (cfr Grafico 1): l’importo della rata, aumenta cioè in misura esponenziale rispetto alla variazione (in aumento) del tasso d’interesse e questo è dovuto proprio al fenomeno anatocistico di “capitalizzazione degli interessi” insito nel calcolo del suo valore.
ANATOCISMO NEL PIANO ALLA FRANCESE: DIMOSTRAZIONE EMPIRICA
Proseguiamo la nostra indagine finalizzata a rispondere in maniera non aribitraria alla “domanda principale” con una analisi sul piano empirico della questione.
Al fine di convincere della risposta i lettori più scettici, procederemo in tal senso ad effettuare un parallelismo tra gli interessi generati mediante il rimborso di un prestito di € 50.000,00 da effettuare con un piano di ammortamento redatto “alla francese” (in regime composto) mediante il pagamento di 20 rate scadenti in via posticipata trimestralmente al tasso dell’ 8%, con divisore TAN 365 gg, ed uno scoperto di c/c pari (quindi un debito iniziale), anch’esso all’inizio pari ad €50.000, su cui vi siano versamenti periodici del correntista pari all’ammontare delle rate da pagare nel mutuo e capitalizzazione trimestrale (anatocismo) degli interessi debitori via via maturati, calcolati al tasso del 8% annuo, e vedremo se i risultati coincidono. Se gli interessi totali maturati sul conto corrente saranno uguali al totale degli interessi da corrispondere per estinguere il mutuo allora la tesi (esiste anatocismo nel mutuo alla francese) sarà verificata.
Cominciamo con il verirficare, mediante l’applicazione della 2.10 e l’ausilio di un foglio di calcolo o di un software dedicato, che l’importo della rata fissa del mutuo sarà pari ad €3.057,84. Di seguito si riporta il relativo piano di ammortamento.
Tavola 1: piano di ammortamento alla francese redatto in regime di capitalizzazione composta di un mutuo di €50.000 da rimborsare con rate trimestrali posticipate al tasso annuo nominale dell’8%
| Nr. | Scadenza Rata | Importo Rata | Quota Interessi | Quota Capitale | Debito Residuo | Debito Estinto | T.A.N. | T.A.E. |
| 0 | 31/12/2010 | 0,00 | 0,00 | 0,00 | 50.000,00 | 0,00 | 8,00% | 8,24% |
| 1 | 31/03/2011 | 3.057,84 | 986,30 | 2.071,54 | 47.928,46 | 2.071,54 | 8,00% | 8,24% |
| 2 | 30/06/2011 | 3.057,84 | 955,94 | 2.101,90 | 45.826,56 | 4.173,44 | 8,00% | 8,24% |
| 3 | 30/09/2011 | 3.057,84 | 924,06 | 2.133,78 | 43.692,79 | 6.307,21 | 8,00% | 8,24% |
| 4 | 31/12/2011 | 3.057,84 | 881,04 | 2.176,80 | 41.515,99 | 8.484,01 | 8,00% | 8,24% |
| 5 | 31/03/2012 | 3.057,84 | 825,78 | 2.232,06 | 39.283,93 | 10.716,07 | 8,00% | 8,24% |
| 6 | 30/06/2012 | 3.057,84 | 781,39 | 2.276,45 | 37.007,47 | 12.992,53 | 8,00% | 8,24% |
| 7 | 30/09/2012 | 3.057,84 | 744,19 | 2.313,65 | 34.693,83 | 15.306,17 | 8,00% | 8,24% |
| 8 | 31/12/2012 | 3.057,84 | 697,67 | 2.360,17 | 32.333,66 | 17.666,34 | 8,00% | 8,24% |
| 9 | 31/03/2013 | 3.057,84 | 637,81 | 2.420,03 | 29.913,63 | 20.086,37 | 8,00% | 8,24% |
| 10 | 30/06/2013 | 3.057,84 | 596,63 | 2.461,21 | 27.452,43 | 22.547,57 | 8,00% | 8,24% |
| 11 | 30/09/2013 | 3.057,84 | 553,56 | 2.504,28 | 24.948,15 | 25.051,85 | 8,00% | 8,24% |
| 12 | 31/12/2013 | 3.057,84 | 503,06 | 2.554,78 | 22.393,37 | 27.606,63 | 8,00% | 8,24% |
| 13 | 31/03/2014 | 3.057,84 | 441,73 | 2.616,11 | 19.777,26 | 30.222,74 | 8,00% | 8,24% |
| 14 | 30/06/2014 | 3.057,84 | 394,46 | 2.663,38 | 17.113,88 | 32.886,12 | 8,00% | 8,24% |
| 15 | 30/09/2014 | 3.057,84 | 345,09 | 2.712,75 | 14.401,14 | 35.598,86 | 8,00% | 8,24% |
| 16 | 31/12/2014 | 3.057,84 | 290,39 | 2.767,45 | 11.633,69 | 38.366,31 | 8,00% | 8,24% |
| 17 | 31/03/2015 | 3.057,84 | 229,49 | 2.828,35 | 8.805,33 | 41.194,67 | 8,00% | 8,24% |
| 18 | 30/06/2015 | 3.057,84 | 175,62 | 2.882,22 | 5.923,12 | 44.076,88 | 8,00% | 8,24% |
| 19 | 30/09/2015 | 3.057,84 | 119,44 | 2.938,40 | 2.984,71 | 47.015,29 | 8,00% | 8,24% |
| 20 | 31/12/2015 | 3.044,90 | 60,18 | 2.984,71 | 0,00 | 50.000,00 | 8,00% | 8,24% |
E’ facile verificare come il totale degli interessi generati dal nostro piano di ammortamento, sia pari ad €11.143,86.
Adesso replichiamo i movimenti in quota capitale sul nostro conto corrente di esempio immaginando un addebito iniziale della Banca pari ad €50.000,00 (pari all’importo del mutuo) e versamenti periodici, effettuati dal correntista alla fine di ciascun trimestre, pari ad € 3.057,84, ovvero pari all’importo (costante) rata del nostro mutuo d’esempio.
Tavola 2: estratto (iniziale) di conto corrente con addebito iniziale di €50.000,00 ed accrediti trimestrali di €3.057,84 con interessi debitori calcolati al tasso annuo nominale dell’8%
| Data valuta | Dare | Avere | Descrizione operazione | Saldo contabile |
| 31/12/2010 | 50.000,00 | 0,00 | Erogazione mutuo |
-50.000,00 |
| 31/03/2011 | 0,00 | 3.057,84 | Pagamento rata | -46.942,16 |
| 30/06/2011 | 0,00 | 3.057,84 | Pagamento rata | -43.884,32 |
| 30/09/2011 | 0,00 | 3.057,84 | Pagamento rata | -40.826,48 |
| 31/12/2011 | 0,00 | 3.057,84 | Pagamento rata | -37.768,64 |
| 31/03/2012 | 0,00 | 3.057,84 | Pagamento rata | -34.710,80 |
| 30/06/2012 | 0,00 | 3.057,84 | Pagamento rata | -31.652,96 |
| 30/09/2012 | 0,00 | 3.057,84 | Pagamento rata | -28.595,12 |
| 31/12/2012 | 0,00 | 3.057,84 | Pagamento rata | -25.537,28 |
| 31/03/2013 | 0,00 | 3.057,84 | Pagamento rata | -22.479,44 |
| 30/06/2013 | 0,00 | 3.057,84 | Pagamento rata | -19.421,60 |
| 30/09/2013 | 0,00 | 3.057,84 | Pagamento rata | -16.363,76 |
| 31/12/2013 | 0,00 | 3.057,84 | Pagamento rata | -13.305,92 |
| 31/03/2014 | 0,00 | 3.057,84 | Pagamento rata | -10.248,08 |
| 30/06/2014 | 0,00 | 3.057,84 | Pagamento rata | -7.190,24 |
| 30/09/2014 | 0,00 | 3.057,84 | Pagamento rata | -4.132,40 |
| 31/12/2014 | 0,00 | 3.057,84 | Pagamento rata | -1.074,56 |
| 31/03/2015 | 0,00 | 3.057,84 | Pagamento rata | 1.983,28 |
| 30/06/2015 | 0,00 | 3.057,84 | Pagamento rata | 5.041,12 |
| 30/09/2015 | 0,00 | 3.057,84 | Pagamento rata | 8.098,96 |
| 31/12/2015 | 0,00 | 3.044,90 | Pagamento rata | 11.143,86 |
Osservazione. Dalla Tavola 2 si vede che, alla fine dei 20 trimestri di riferimento, il saldo del nostro conto corrente sarà a credito del correntista per un importo pari ad €11.143,86: questo importo coincide esattamente con gli interessi totali generati dal nostro piano di ammortamento di esempio. La ragione è che non ancora abbiamo calcolato gli interessi che il nostro correntista dovrà versare alla fine di ciascun trimestre, cosa che faremo tra poco.
L’obiettivo di questa verifica “empirica” della presenza di anatocismo nel piano di ammortamento alla francese, è dimostrare che gli interessi generati su un conto corrente su cui è dichiaratamente praticato l’anatocismo, ovvero l’addebito periodico (trimestrale in questo caso) degli interessi maturati alla fine di ciascun trimestre, risultano essere esattamente uguali a quelli generati dall’ammortamento alla francese (realizzato in regime di interessi composti).
Cominciamo quindi con il calcolare gli interessi che la Banca addebiterà sul nostro conto corrente alla fine del primo trimestre di riferimento mediante il consueto schema di calcolo degli interessi su un conto corrente: (TAN/365)*Numeri debitori, dove nel nostro caso TAN=8,00% e Numeri debitori =Saldo x gg. trimestre, che nel nostro caso fornisce il numero 4.500.000=50.000×90, essendo 90 i giorni del trimestre intercorrente tra il 31/12/2010-31/03/2011 e 50.000 il nostro saldo debitore iniziale.
Il risultato sarà quindi pari a (8,00%/365)x4.500.000=€986,30. Abbiamo così ritrovato la quota interessi da corrispondere sulla prima rata del nostro mutuo (cfr. Tavola 1).
A questo punto dobbiamo addebitare questi interessi nel nostro conto corrente, sicché il saldo dello stesso, alla fine del I trimestre di riferimento, risulterà pari ad €47.928,46.
| Data valuta | Dare | Avere | Descrizione operazione | Saldo contabile |
| 31/12/2010 | 50.000,00 | 0,00 | Erogazione mutuo | -50.000,00 |
| 31/03/2011 | 0,00 | 3.057,84 | Pagamento rata | -46.942,16 |
| 31/03/2011 | 986,30 | 0,00 | Addebito interessi I trim.2011 | -47.928,46 |
Si noti una cosa: il saldo del conto corrente su cui abbiamo appena capitalizzato gli interessi maturati nel I trimestre, coincide esattamente con il debito residuo risultante nel nostro piano di ammortamento alla francese dopo il pagamento della prima rata.
Ora non ci resta che calcolare gli interessi dovuti su questo nuovo saldo di conto corrente per il II trimesttre 2011.
Seguendo il consueto schema di calcolo, calcoliamo dapprima i numeri debitori del saldoconto per valuta: essi saranno pari a 47.928,46×91=4.361.489,985
dove 47.928,46 è il saldoconto all’inizio del II trimestre 2011 e 91 sono i giorni intercorrenti tra la data del 31/03/2011 e quella del 30/06/2011.
A questo punto, per il calcolo degli interessi che la Banca addebiterà sul II trimestre 2011, non ci resta che effettuare il seguente calcolo: (8,00%/365)/436.1489,985=€955,94.
Si noti come “casualmente”, questi interessi coincidano di nuovo esattamente con quelli da versare con la seconda rata del nostro mutuo (si veda ancora la Tavola 1). Ora non ci resta che “addebitare” questi interessi sul nostro conto corrente e constatare come “magicamente” il saldo coincida esattamente con il debito residuo (€45.826,56) risultante dal nostro piano di ammortamento dopo (il corsivo non è un errore di battitura) il pagamento della seconda rata.
| Data valuta | Dare | Avere | Descrizione operazione | Saldo contabile |
| 31/12/2010 | 50.000,00 | 0,00 | Erogazione mutuo | -50.000,00 |
| 31/03/2011 | 0,00 | 3.057,84 | Pagamento rata | -46.942,16 |
| 31/03/2011 | 986,30 | 0,00 | Addebito interessi I trim.2011 | -47.928,46 |
| 30/06/2011 | 0,00 | 3.057,84 | Pagamento rata | -44.870,62 |
| 30/06/2011 | 955,94 | 0,00 | Addebito interessi II trim.2011 | -45.826,56 |
Adesso non ci resta che replicare lo stesso ragionamento per il III trimestre del 2011 e per tutti gli altri a seguire fino al IV trimestre del 2015, data in cui si estingue il nostro finanziamento ed anche il nostro conto corrente.
Procedendo nel consueto modo, troviamo che i numeri debitori maturati sul saldo di c/c per il III trimestre sono pari a 4.216.043,92 i giorni valuta sono 92 (numero di giorni intercorrenti tra la data del 30/06/2011 e quella del 30/09/2011) e gli interessi passivi, maturati al TAN (tasso annuo nominale) dell’8,00% saranno pari ad €924,06.
Ancora(!) una volta, notiamo come il saldo conto alla fine del III trimestre, che risulterà essere pari ad €43.692,79, coincida esattamente con il debito residuo del nostro piano di ammortamento dopo il pagamento della III rata di mutuo.
| Data valuta | Dare | Avere | Descrizione operazione | Saldo contabile |
| 31/12/2010 | 50.000,00 | 0,00 | Erogazione mutuo | -50.000,00 |
| 31/03/2011 | 0,00 | 3.057,84 | Pagamento rata | -46.942,16 |
| 31/03/2011 | 986,30 | 0,00 | Addebito interessi I trim.2011 | -47.928,46 |
| 30/06/2011 | 0,00 | 3.057,84 | Pagamento rata | -44.870,62 |
| 30/06/2011 | 955,94 | 0,00 | Addebito interessi II trim.2011 | -45.826,56 |
| 30/09/2011 | 0,00 | 3.057,84 | Pagamento rata | -42.768,72 |
| 30/09/2011 | 924,06 | 0,00 | Addebito interessi III trim.2011 | -43.692,79 |
Bene. A questo punto lasciamo al “lettore volenteroso” la verifica dei calcoli successivi, avvertendolo che l’anno 2012 è bisestile per cui il divisore TAN, dovrà essere 366 e non 365. Noi ci affideremo ad un comodo foglio di calcolo che, una volta inserite tutte le necessarie formule, fornirà il prospetto finale rappresentato nella Tavola 3, dove sono riportati anche tutti gli elementi di calcolo necessari alla verifica sperimentale in commento.
| Data valuta | Dare | Avere | Descrizione operazione | Saldo contabile | Numeri debitori | Interessi |
| 31/12/2010 | 50.000,00 | 0,00 | Erogazione mutuo | -50.000,00 | ||
| 31/03/2011 | 0,00 | 3.057,84 | Pagamento rata | -46.942,16 | 4.500.000,00 | 986,30 |
| 31/03/2011 | 986,30 | 0,00 | Addebito interessi I trim.2011 | -47.928,46 | 0,00 | 0,00 |
| 30/06/2011 | 0,00 | 3.057,84 | Pagamento rata | -44.870,62 | 4.361.489,98 | 955,94 |
| 30/06/2011 | 955,94 | 0,00 | Addebito interessi II trim.2011 | -45.826,56 | 0,00 | 0,00 |
| 30/09/2011 | 0,00 | 3.057,84 | Pagamento rata | -42.768,72 | 4.216.043,92 | 924,06 |
| 30/09/2011 | 924,06 | 0,00 | Addebito interessi III trim.2011 | -43.692,79 | 0,00 | 0,00 |
| 31/12/2011 | 0,00 | 3.057,84 | Pagamento rata | -40.634,95 | 4.019.736,57 | 881,04 |
| 31/12/2011 | 881,04 | Addebito interessi I trim.2011 | -41.515,99 | 0,00 | 0,00 | |
| 31/03/2012 | 0,00 | 3.057,84 | Pagamento rata | -38.458,15 | 3.777.954,81 | 825,78 |
| 31/03/2012 | 825,78 | Addebito interessi I trim.2012 | -39.283,93 | 0,00 | 0,00 | |
| 30/06/2012 | 0,00 | 3.057,84 | Pagamento rata | -36.226,09 | 3.574.837,58 | 781,39 |
| 30/06/2012 | 781,39 | Addebito interessi II trim.2012 | -37.007,47 | 0,00 | 0,00 | |
| 30/09/2012 | 0,00 | 3.057,84 | Pagamento rata | -33.949,63 | 3.404.687,67 | 744,19 |
| 30/09/2012 | 744,19 | Addebito interessi III trim.2012 | -34.693,83 | 0,00 | 0,00 | |
| 31/12/2012 | 0,00 | 3.057,84 | Pagamento rata | -31.635,99 | 3.191.832,24 | 697,67 |
| 31/12/2012 | 697,67 | Addebito interessi IV trim.2012 | -32.333,66 | 0,00 | 0,00 | |
| 31/03/2013 | 0,00 | 3.057,84 | Pagamento rata | -29.275,82 | 2.910.029,13 | 637,81 |
| 31/03/2013 | 637,81 | Addebito interessi I trim.2013 | -29.913,63 | 0,00 | 0,00 | |
| 30/06/2013 | 0,00 | 3.057,84 | Pagamento rata | -26.855,79 | 2.722.140,47 | 596,63 |
| 30/06/2013 | 596,63 | Addebito interessi II trim.2013 | -27.452,43 | 0,00 | 0,00 | |
| 30/09/2013 | 0,00 | 3.057,84 | Pagamento rata | -24.394,59 | 2.525.623,11 | 553,56 |
| 30/09/2013 | 553,56 | Addebito interessi III trim.2013 | -24.948,15 | 0,00 | 0,00 | |
| 31/12/2013 | 0,00 | 3.057,84 | Pagamento rata | -21.890,31 | 2.295.229,46 | 503,06 |
| 31/12/2013 | 503,06 | Addebito interessi IV trim.2013 | -22.393,37 | 0,00 | 0,00 | |
| 31/03/2014 | 0,00 | 3.057,84 | Pagamento rata | -19.335,53 | 2.015.403,33 | 441,73 |
| 31/03/2014 | 441,73 | Addebito interessi I trim.2014 | -19.777,26 | 0,00 | 0,00 | |
| 30/06/2014 | 0,00 | 3.057,84 | Pagamento rata | -16.719,42 | 1.799.730,89 | 394,46 |
| 30/06/2014 | 394,46 | Addebito interessi II trim.2014 | -17.113,88 | 0,00 | 0,00 | |
| 30/09/2014 | 0,00 | 3.057,84 | Pagamento rata | -14.056,04 | 1.574.477,34 | 345,09 |
| 30/09/2014 | 345,09 | Addebito interessi III trim.2014 | -14.401,14 | 0,00 | 0,00 | |
| 31/12/2014 | 0,00 | 3.057,84 | Pagamento rata | -11.343,30 | 1.324.904,42 | 290,39 |
| 31/12/2014 | 290,39 | Addebito interessi IV trim.2014 | -11.633,69 | 0,00 | 0,00 | |
| 31/03/2015 | 0,00 | 3.057,84 | Pagamento rata | -8.575,85 | 1.047.031,65 | 229,49 |
| 31/03/2015 | 229,49 | Addebito interessi I trim.2015 | -8.805,33 | 0,00 | 0,00 | |
| 30/06/2015 | 0,00 | 3.057,84 | Pagamento rata | -5.747,49 | 801.285,16 | 175,62 |
| 30/06/2015 | 175,62 | Addebito interessi II trim.2015 | -5.923,12 | 0,00 | 0,00 | |
| 30/09/2015 | 0,00 | 3.057,84 | Pagamento rata | -2.865,28 | 544.926,63 | 119,44 |
| 30/09/2015 | 119,44 | Addebito interessi III trim.2015 | -2.984,71 | 0,00 | 0,00 | |
| 31/12/2015 | 0,00 | 3.044,90 | Pagamento rata | 60,19 | 274.593,46 | 60,18 |
| 31/12/2015 | 60,18 | 0,00 | Addebito interessi IV trim.2015 | 0,00 | 0,00 | 0,00 |
A questo punto la nostra “verifica empirica” è terminata e la nostra ipotesi di partenza, ovvero che nell’ammortamento di un prestito alla francese a rata costante esiste anatocismo, è verificata. In altre parole: l’ipotesi di partenza, ovvero quello dell’esistenza di “interessi calcolati sugli interessi” nei piani di ammortamento alla francese a rata costante, è adesso una tesi dimostrata e, sotto il profilo squisitamente matematico, non vi è null’altro da aggiungere se non quanto segue.
Spesso, si confonde la questione dell’anatocismo nel piano di ammortamento alla francese con la questione legata alla discrasia tra il TAN (tasso annuo nominale) ed il TAE (tasso annuo effettivo) che si realizza in caso di pagamenti delle rate infrannuali. Si tratta in vero di questioni totalmente distinte, se pur correlate sotto il profilo della trasparenza nelle condizioni contrattuali.
Nel regime ad interessi composto infatti, dato un certo TAN (tasso annuo nominale), il TAE (tasso annnuo effettivo) risultate è dato dalla seguente relazione:
T.A.E.= {( 1+\frac{T.A.N.}{periodi capitaliz.} )} ^{periodi capitaliz.}-1
Sostituendo i valori del nostro esempio con le variaibli TAN=8,00% e periodi di capitalizzazione (infrannuali)= 4, troveremo un TAE=8,24%.
Per come infatti è definita la struttura del piano di ammortamento nel regime composto, il pagamento di rate infrannuali non rappresenta altro che una sorta di “anticipazione” rispetto al pagamento dell’unica rata teorica (annuale) dovuta. Bisogna però qui fissare l’attenzione su una cosa: la formula che calcola il T.A.E. sopra data, si fonda, ancora, sul regime ad interesse composto e calcola un “tasso annuo effettivo“: l’ipotesi sottostante è che, in ogni caso, sia “legittimo” capitalizzare gli interessi almeno una volta all’anno ma questo è tuttavia vietato dalle disposizioni normative attuali come argomentato in premessa.
La discrasia tra TAN e TAE, da molti Autori e Consulenti tecnici declamata quale “unica conseguenza” dell’adozione di un piano di ammortamento alla francese con rate infrannuali, in realtà quindi nulla ci dice a proposito del reale innalzamento degli interessi pagati quando si pagano rate calcolate con gli algoritmi con cui sono costruiti in genere i piani di ammortamento alla francese.
Si noti in tal senso che se il piano di rimborso si chiudesse entro l’anno, allora la discrasia tra TAN e TAE fornirebbe l’esatta misura degli “interessi sugli interessi” maturati e questo perché, come evidente da quanto sopra, per “periodi unitari” gli interessi calcolati con il regime composto coincidono con quelli calcolati in regime semplice. Quando però ci si trova dinanzi a piani di ammortamento ultrannuali se non ultradecennali, il TAE come sopra definito non fornisce in realtà alcuna informazione sul fenomeno anatocistico insito nei comuni piani di ammortamento.
CONCLUSIONI
A questo punto dovrebbe essere chiaro, almeno a chi dopo aver letto tutto l’articolo è arrivato fin qui, perché esiste anatocismo nei piani di ammortamento alla francese e negarlo è frutto di puro arbitrio intellettuale.
La stragrande maggioranza delle argomentazioni con cui si nega il fenomeno anatocistico nell’ammortamento francese (in regime di interessi composto ndr.) poggia infatti su delle osservazioni la cui “ingenutà” risulta per certi versi sconcertante.
In generale si nega la presenza di anatocismo nel piano di ammortamento alla francese perché esso funzionerebbe nel seguente modo:
-
Si calcolano gli interessi sul debito iniziale e si determina la quota interessi della prima rata.
-
Si sottrae la quota interesse così individuata dalla rata costante e si ricava per differenza la quota capitale della prima rata.
-
La quota capitale di tale prima rata si porta in detrazione del debito iniziale e si ottiene il nuovo debito residuo.
-
Sul debito residuo riveniente dalla prima rata si calcola la quota interessi della seconda rata.
-
Dalla rata costante si ricava per differenza la quota capitale della seconda rata.
-
La quota capitale della seconda rata va a ridurre il debito residuo su cui si calcola la quota interessi della terza rata e così via fino all’ultima rata.
Dal ché ne discenderebbe che:
“Ciò non comporta capitalizzazione degli interessi, atteso che gli interessi conglobati nella rata successiva sono a loro volta calcolati unicamente sulla residua quota di capitale, ovverosia sul capitale originario detratto l’importo già pagato con la rata o le rate precedenti, e unicamente per il periodo successivo al pagamento della rata immediatamente precedente“(cfr. Tribunale di Siena, 17 luglio 2014).
Lette alla luce di tutto quanto sopra, queste argomentazioni non possono che svelarsi in tutta la loro fallacia: a quanto pare, a nessuno di questi “brillanti matematici” è venuto in mente di indagare più a fondo la struttura matematica del piano di ammortamento alla francese che – come ha avuto modo di capire chi è arrivato vivo fin qui – è tutt’altro che banale, per andare a verificare quindi:
-
innanzitutto, come si calcola davvero l’importo della rata costante nell’ammortamento francese, senza utilizzare alcun software, applicazione web e/o foglio di calcolo: si scoprirebbe forse che bisogna studiare bene prima di rispondere.
-
In che modo, per conseguenza del calcolo della rata, vengono calcolate le quote capitale e quindi il debito residuo (formula 3.4) e le quote interessi (formula 3.5).
In altre parole: fondamentalmente, per negare l’anatocismo nei comuni piani di ammortamento alla francese, si parte dal presupposto che per verificare o meno la presenza di “interessi calcolati sugli interessi” in siffatti piani di amomortamento, ci si possa limitare alla verifica della 2.4, così trovando conferma in quella che evidentemente non può essere che – al più – una mera “congettura“.
Una congettura che poi a bene vedere non può davvero nemmeno definirsi tale dal momento che una congettura è qualcosa sulla cui validità non ci si può pronunciare a causa di limiti della conoscenza umana (es. che l’universo sia infinito è attualmente una congettura) nel mentre l’affermazione “nel piano di ammortamento alla francese (redatto in regime di itneressi composti) non c’è anatocismo” è una affermazione del tutto falsa, non elevabile al rango di congettura in quanto confutabile e senza neanche poter sperare nell’attribuzione di una medaglia fields, data la natura non estremamente banale dell’argomento ma certo tutt’altro che “di frontiera”, almeno da un punto di vista matematico.
Certo: neanche questo contributo convincerà chi non vuol convincersi perché ci sarà sempre un “cavillo” sul quale qualcuno tenterà di fondare la dimostrazione del fatto che 2×2=5. Ma un fatto resta:
NELL’AMMORTAMENTO FRANCESE (in regime di interessi composto), NELLA BASE DI CALCOLO DEGLI INTERESSI DA CORRISPONDERE SU CIASCUNA RATA, VENGONO SOMMATI GLI INTERESSI CORRISPOSTI SULLE RATE PRECEDENTI E QUESTO REALIZZA PROPRIO L’ANATOCISMO (formula 3.5).
E NELL’AMMORTAMENTO C.D “ALL’ITALIANA”? ESISTE ANATOCISMO?
Sebbene spesso si prenda il piano di ammortamento “a quote capitali costanti” o “all’italiana” che dir si voglia, come esempio di piano di ammortamento scevro da anatocismo, la risposta è ancora SI: ANCHE NEL PIANO DI AMMORTAMENTO ALL’ITALIANA SI VERIFICA ANATOCISMO. Infatti anche per esso è possibile verificare come la quota interessi venga calcolata attraverso la 3.5, a fronte di una rata per il calcolo della quale non si pone alcun “vincolo”. Certo, quello italiano risulta il più semplice da calcolare ma comunque non vi è nulla nella sua struttura matematico-attuariale che possa evitare il fenomeno anatocistico.
Per capire perché, al di là delle evidenze matematiche, bisogna capire una cosa: “pagare gli interessi rata per rata” equivale a privarsi di una disponibilità di denaro che, “in un mondo governato dal regime dell’interesse semplice” dovrebbe restare nella disponibilità del mutuatario.
In altre parole, nei comuni piani di ammortamento la generazione di interessi anatocistici è insita proprio nel fatto che si pagano gli interessi su ciascuna rata. Affinché non vi sia “capitalizzazione” degli interessi, questi dovrebbero essere si conteggiati, ma restare nella disponibilità del debitore ed essere corrisposti soltanto alla fine del periodo di rimborso nel mentre il debito residuo dovrebbe diminuire non già attraverso la formula 3.4 ma dell’intera rata: solo così si eviterebbe in maniera “semplice” l’anatocismo senza cioè il ricorso ad algoritmi di calcolo più sofisticati che “depurino” la base di calcolo degli interessi calcolati rata per rata dall’anatocismo.
E SE VOLESSIMO QUANTIFICARE L’ANATOCISMO NELL’AMMORTAMENTO FRANCESE?
Esistono diverse tecniche per farlo: una assai semplice, che tuttavia non porta a risultati definitivi ed ha delle limitazioni ma che almeno fa capire i termini della questione, consiste nel “conteggiare a parte” gli interessi via via maturati facendo nel contempo diminuire il debito residuo dell’intera rata pagata, non della sola “quota capitale”, evitando così la capitalizzazione degli interessi e quindi l’anatocismo. Si avranno in tal modo due distinte linee di debito: una in “quota capitale” ed una “in quota interessi” ed il debito residuo complessivo, tempo per tempo, sarà dato dalla somma tra i due debiti sopra definiti.
Riprendiamo il nostro piano di ammortamento di esempio.
| Scadenza Rata | Importo Rata | Quota Capitale | Debito residuo in quota capitale | Vecchi Interessi | Nuovi Interessi | Debito residuo in quota Interessi | DEBITO RESIDUO TOTALE |
| 31/12/2010 | 0,00 | 0,00 | 50.000,00 | 0,00 | |||
| 31/03/2011 | 3.057,84 | 3.057,84 | 46.942,16 | 986,30 | 986,30 | 986,30 | 47.928,46 |
| 30/06/2011 | 3.057,84 | 3.057,84 | 43.884,32 | 955,94 | 936,27 | 1.922,57 | 45.806,89 |
| 30/09/2011 | 3.057,84 | 3.057,84 | 40.826,48 | 924,06 | 884,90 | 2.807,47 | 43.633,95 |
| 31/12/2011 | 3.057,84 | 3.057,84 | 37.768,64 | 881,04 | 823,24 | 3.630,71 | 41.399,35 |
| 31/03/2012 | 3.057,84 | 3.057,84 | 34.710,80 | 828,04 | 753,30 | 4.384,02 | 39.094,82 |
| 30/06/2012 | 3.057,84 | 3.057,84 | 31.652,96 | 783,53 | 692,31 | 5.076,33 | 36.729,29 |
| 30/09/2012 | 3.057,84 | 3.057,84 | 28.595,12 | 746,23 | 638,26 | 5.714,59 | 34.309,71 |
| 31/12/2012 | 3.057,84 | 3.057,84 | 25.537,28 | 699,58 | 576,60 | 6.291,20 | 31.828,48 |
| 31/03/2013 | 3.057,84 | 3.057,84 | 22.479,44 | 637,81 | 503,75 | 6.794,95 | 29.274,39 |
| 30/06/2013 | 3.057,84 | 3.057,84 | 19.421,60 | 596,63 | 448,36 | 7.243,30 | 26.664,90 |
| 30/09/2013 | 3.057,84 | 3.057,84 | 16.363,76 | 553,56 | 391,62 | 7.634,93 | 23.998,69 |
| 31/12/2013 | 3.057,84 | 3.057,84 | 13.305,92 | 503,06 | 329,97 | 7.964,89 | 21.270,81 |
| 31/03/2014 | 3.057,84 | 3.057,84 | 10.248,08 | 441,73 | 262,47 | 8.227,36 | 18.475,44 |
| 30/06/2014 | 3.057,84 | 3.057,84 | 7.190,24 | 394,46 | 204,40 | 8.431,77 | 15.622,01 |
| 30/09/2014 | 3.057,84 | 3.057,84 | 4.132,40 | 345,09 | 144,99 | 8.576,75 | 12.709,15 |
Si veda come gli interessi ed il debito residuo totale coincindano con l’originario piano di ammortamento solo per la prima rata: dopodiché i nuovi interessi sono sempre più bassi in conseguenza del fatto che nel piano di ammortamento originario (alla francese) c’è la capitalizzazione degli interessi mentre nel nuovo no.
Si confronti adesso il debito residuo alla data del 30/09/2014: esso risulta essere dato dalla somma tra il “Debito in quota capitale” che risulta essere pari ad €4.132,40 ed il “Debito in quota interessi” che risulta essere pari ad €8.576,75 per un totale di €12.709,15 anziché €14.401,14 come nel vecchio piano di ammortamento.
AVVERTENZA
Se si proseguisse come sopra fino alla rata 20 (scadente al 31/12/2015) del piano di ammortamento orginario, ad un certo punto si arriverà ad avere un “Debito residuo in quota capitale negativo”: tale circostanza non deve affatto sorprendere in quanto dovuta al fatto che l’importo della rata orignaria è calcolata con un algoritmo (formula 2.9) che ingloba del suo importo gli interessi anatocistici.
Per evitare questo problema, si potrebbe, aiutandosi con un foglio di calcolo, procedere “per tentativi” fino a trovare l’importo della rata “corretto”: questo però potrebbe richiedere molto tempo.
Ma questo non è l’unico problema: alla base di tutta la matematica finanziaria attuariale c’è il concetto che “il possesso di una somma di denaro genera interessi”. Inoltre, esiste anche un motivo di tipo giuridico che rende incerto l’esito di un siffatto calcolo in caso di contenzioso che è l’art. 1194 c.c. il quale stabilisce che:
“Il debitore non può imputare il pagamento al capitale, piuttosto che agli interessi e alle spese, senza il consenso del creditore. Il pagamento fatto in conto di capitale e d’interessi deve essere imputato prima agli interessi”.
QUINDI COME SI PUO’ GENERARE UN PIANO DI AMMORTAMENTO A RATA COSTANTE CON CUI SI PAGHINO RATA PER RATA CAPITALE E INTERESSI MA SENZA GENERARE ANATOCISMO?
La riposta a questo domanda è semplice: utilizzando, per il calcolo della rata di rimborso, il regime dell’interesse semplice! Questo argomento tuttavia richiede una trattazione matematica specifica ed in questo articolo ci siamo già dilungati abbastanza. La costruzione di piani di ammortamento in regime di interesse semplice presenta infatti una difficoltà tecnica superiore a quella che si ha nel regime di interesse composto.
La ragione è nelle proprietà matematiche di cui godono le funzioni fattore di montante e fattore di sconto nel RIC ed in particolare in quella nota come “proprietà di scindibilità“, che permette di stabilire l’equivalenza finanziaria tra importi diversi disponibili ad epoche diverse in manira estremamente agevole. Torneremo in ogni caso sull’argomento. Per il momento speriamo di aver chiarito ogni dubbio sul fatto – che è un fatto e non un’opinione – che nel piano di ammortamento alla francese (redatto in regime di capitalizzazione composta ndr.) esiste anatocismo. Per il momento rimandiamo il lettore interessato ad approfondire all’argomento alla bibliografia di riferimento, sperando che in futuro la questione possa essere dibattuta nella aule dei Tribunali con minore superficialità.
E LA GIURISPRUDENZA COSA NE PENSA?
Dopo avere in maggioranza negato l’esistenza del fenomeno anatocistico nei piani di ammortamento alla francese (redatti in regime di interesse composto), ultimamente diverse pronunce di merito riconoscono il problema, sanzionando il comportamento di Banche ed Intermediari finanziari che, applicando siffatta tecnica di ammortamento, realizzano illeggittimamente un occulto (e notevole) aumento dei costi in quota interesse per il debitore con violazione degli art. 1283, 1284 c.c. e soprattutto degli 116 e 117 del T.u.b. in materia di trasparenza contrattuale. Si veda in tal senso tra le ultime pronunce:
- Tribunale di Napoli, sent. n. 1558/2018 del 13 febbraio 2018, Est. Alienante
- Tribunale di Lucca sent. del 10 maggio, 2018. Est. Mancini
Per una disamina di tutte le sentenze che riconoscono (sebbene non sempre con i giusti connotati è da dire) l’anatocismo nel piano di ammortamento alla francese, nonché degli articoli che approfondiscono l’argomento, si veda la sezione speciale del sito dedicata all’argomento.
Per eventuali informazioni, chiarimenti o confronti sull’argomento, o su come si faccia a redigere un piano di ammortamento in regime di interesse semplice, potete invece scrivere a info@verifichefinanziamenti.
Biglografia di riferimento
- Lezioni di matematica finanziaria classica e moderna (Fabrizio Cacciafesta-Giappichelli Editore)
- Anatocismo e ammortamento di mutui alla francese in capitalizzazione semplice (Antonio Annibali – Carla Barracchini – Alessandro Annibali)
- Sull’anatocismo nell’ammortamento francese (Paola Fersini, Gennario Olivieri -pubblicato sulla Rivista della Associazione Nazionale Banche Private 2/2015).

Dopo la laurea, frequenta con profitto il Master universitario di II livello in “Matematica per le Applicazioni” presso il Dipartimento di matematica dell’Università di Bologna
Dottore Commercialista e Revisore legale.
Consulente tecnico materia di contenzioso bancario
E’ iscritto nell’elenco dei Gestori della Crisi da Sovraindebitamento.
I NOSTRI SOFTWARE
Sub-domains
Your Text
Your Text
Your Text









 Benevento (BN)
Benevento (BN) +39 0824 317664
+39 0824 317664











